Calcul vectoriel
- Tutux
- 16 mai 2023
- 4 min de lecture
Dernière mise à jour : 17 mai 2023
Le calcul vectoriel ou "analyse vectorielle" est une branche des mathématiques qui étudie les champs de scalaires et de vecteurs suffisamment réguliers des espaces euclidiens (voir définition plus loin).
L'importance du calcul vectoriel provient de son utilisation intensive en physique et dans les sciences de l'ingénieur. C'est de ce point de vue que nous le présenterons, et c'est pourquoi nous nous limiterons le plus souvent au cas de l'espace usuel à trois dimensions. Dans ce cadre, un champ de vecteurs associe à chaque point de l'espace un vecteur (à trois composantes réelles), tandis qu'un champ de scalaires y associe un réel.
1 ENSEMBLE DES VECTEURS
Définitions :
Un vecteur est un objet géométrique d'un espace vectoriel qu'on représente par une flèche d'une certaine longueur pointant dans une direction de cet espace. On peut utiliser un repère pour décrire cet objet géométrique par des nombres abstraits ordonnés dans une "matrice colonne" :

Ces nombres peuvent donc varier en fonction du repère que l'on utilise ainsi que de sa dimension unitaire représentée par ce qu'on appelle des vecteurs de base :

On verra dans la section du calcul tensoriel qu'un vecteur est en fait un tenseur d'ordre 1 qu'on reproduit en répétant les vecteurs de base autant de fois que nécessaire.
Ici le vecteur a les composantes (4,2,6):

En effectuant une transformation du système de coordonnées en doublant la norme des vecteurs de base, les nouvelles composantes du vecteur dans ce nouveau système de coordonnées diminue et ont pour valeur (2,1,3).
Donc lorsqu'on opère une transformation du système de coordonnées en augmentant la longueur de ses vecteurs de base, les composantes du vecteur diminuent dans ce nouveau système tandis qu'à l'inverse, si on diminue la longueur des vecteurs de base, ses composantes augmentent.
Une autre manière de décrire un vecteur en utilisant des vecteurs de base consiste à réaliser le produit scalaire du vecteur avec chacun des vecteurs de base. En effet, le produit scalaire entre un vecteur et un vecteur de base est une opération qui mesure la projection du vecteur sur ce vecteur de base:

En effectuant une transformation du système de coordonnées en doublant la norme des vecteurs de base, alors le produit scalaire du vecteur avec chaque vecteur de base dans le nouveau système doublera aussi:

Donc lorsqu'on opère une transformation du système de coordonnées en augmentant la longueur de ses vecteurs de base, on augmente leur produit scalaire avec le vecteur et à l'inverse en diminuant sa norme, on diminue le produit scalaire.
Covariance & Contravariance :
Les composantes d'un vecteur sont dites covariantes lorsque leur transformation suit le même comportement que les vecteurs de base lors d'un changement de système de coordonnées. Cela signifie que si les vecteurs de base sont multipliés par un facteur d'échelle dans une transformation du système de coordonnées, les composantes du vecteur seront également multipliées par le même facteur. En effet, Supposons que nous ayons un vecteur en deux dimensions avec les composantes (2, 3) dans le système de coordonnées standard (x, y):

Si nous effectuons une transformation du système de coordonnées en le redimensionnant par un facteur d'échelle de 2, les vecteurs de base seront également multipliés par ce facteur. Par conséquent, les nouvelles composantes du vecteur dans le nouveau système de coordonnées seront (4, 6) soit :

Les composantes ont été multipliées par le même facteur que les vecteurs de base, ce qui confirme la covariance (représentation en indice).
A l'inverse, les composantes d'un vecteur sont dites contravariantes lorsque leur transformation est inverse à celle des vecteurs de base lors d'un changement de système de coordonnées. Cela signifie que si les vecteurs de base sont multipliés par un facteur d'échelle dans une transformation du système de coordonnées, les composantes du vecteur seront divisées par le même facteur. En effet, prenons maintenant un vecteur en deux dimensions avec les composantes (3, 4) dans le système de coordonnées standard (x, y):
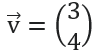
Si nous effectuons une transformation du système de coordonnées en le redimensionnant par un facteur d'échelle de 2, les vecteurs de base seront à nouveau multipliés par ce facteur. Cependant, dans ce cas, les nouvelles composantes du vecteur dans le nouveau système de coordonnées seront (1.5, 2) soit:

Les composantes ont été divisées par le même facteur que les vecteurs de base, ce qui illustre la contravariance (représentation en exposant).
Nous avons donc 2 façons différentes de décrire le même vecteur "v".
Considérons à présent 2 vecteurs différents P et V:

Supposons que l'on multiplie une des composantes contravariantes de P avec une des composantes contravariantes de V, on peut regrouper toutes les combinaisons possibles dans une matrice constituant un exemple de tenseur contravariant de second ordre :


Supposons que l'on multiplie une des composantes covariantes de V avec une des composantes contravariantes de P, on pourra regrouper toutes les combinaisons possibles dans une matrice constituant une description mixte du même tenseur de second ordre:


Un tenseur d'ordre 1 associe un résultat réel (nombre) à chaque vecteur de base:



Un tenseur d'ordre 2 associe un résultat réel à toute combinaison possible de 2 vecteurs de base :

Un tenseur d'ordre 3 associe un résultat réel à toute combinaison possible de 3 vecteurs de base :


Il peut être constitué de la combinaison des composantes de 3 vecteurs :



Propriétés :
Traçons le représentant d'un vecteur y à partir de l'extrémité d'un représentant d'un vecteur x. La flèche dont l'origine est celle du représentant de x et l'extrémité celle du représentant de y détermine un vecteur que nous noterons x+y. L'opération qui associe à tout couple de vecteurs leur somme s'appelle "addition vectorielle".
Additivité et commutativité:


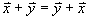
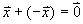
Multiplication par un scalaire:
L'opération qui consiste à effectuer le produit d'un nombre par un vecteur est appelé "multiplication par un scalaire".

2. ESPACES VECTORIELS
Nous appelons "espace vectoriel" un ensemble E d'éléments désignés par x,y... et appelés "vecteurs", muni d'une "structure algébrique vectorielle" définie par la donnée de l'addition (soustraction) vectorielle et la multiplication par un scalaire. Ces deux opérations satisfaisant les lois d'associativité, de commutativité, de distributivité, d'élément neutre et d'opposé:

Pour tout entier positif n, R désignera l'ensemble des n-uplets de nombres disposés en colonne:

et R est à l'évidence munie d'une structure d'espace vectoriel. Les vecteurs de cet espace seront appelés "vecteurs-colonne". Ils seront souvent désignés plus brièvement par:
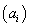
Angles directeurs:
Il est clair qu'un seul angle ne peut décrire la direction d'un vecteur dans l'espace. Nous utilisons alors la notion "d'angles directeurs". Il s'agit de mesurer l'angle du vecteur par rapport à chacun des axes positifs de la base:

Si:

Alors :

Les valeurs :

sont appelées les "cosinus directeurs" de U.

3. ESPACES VECTORIELS EUCLIDIENS





