Calcul différentiel & intégral
- Tutux
- 25 avr. 2023
- 12 min de lecture
Dernière mise à jour : 28 avr. 2023
Nous avons choisi de ne présenter ici que les points absolument nécessaires à la compréhension des outils fondamentaux appliqués à la Physique. Les puristes nous excuseront donc pour l'instant de ne pas présenter certains théorèmes qui peuvent leur sembler indispensables. Nous allons principalement étudier les cas généraux des fonctions réelles à une variable réelle. Les fonctions plus complexes (à plusieurs variables réelles ou complexes, continues ou discrètes) viendront une fois cette partie terminée.
Calcul différentiel
Soit une fonction f réelle à une variable réelle x notée f(x) (nous nous limitons à ce cas de figure pour l'instant et étudierons les dérivées partielles dans des espaces à un nombre de dimensions quelconques plus loin) continue au moins dans un intervalle où se situe l'abscisse a.
Définitions:
- Nous appelons "pente moyenne", ou encore "coefficient directeur" le rapport de la projection orthogonale de deux points de la fonction f non nécessairement continue sur l'axe des abscisses et des ordonnées tel que:

Ce qui se représente sous forme graphique de la manière suivante avec une fonction particulière:


- Nous appelons "nombre dérivé en a" ou "pente instantanée" ou encore "dérivée première", la limite quand h tend vers 0 (si elle existe) du rapport de la projection orthogonale de deux points infiniment proches de la fonction f continue (dans le sens qu'elle ne contient pas de "trous") sur l'axe des abscisses et des ordonnées tel que:

Une interprétation graphique donne donc bien que f'(a) est le coefficient directeur (la pente de la tangente au point d'abscisse a).
Remarque : d signifiant un "différentiel" exprime le fait que nous sous-entendons une différence infiniment petite d'une même quantité.
- Soit f une fonction définie sur un intervalle I et dérivable en tout point a de I, la fonction qui à tout réel a de I associe le nombre f '(a) est appelée "fonction dérivée de f sur I" et est notée f '.

Nous pouvons de la même manière définir les dérivées d'ordre 2 (dérivée d'une dérivée), les dérivées d'ordre 3 (dérivée d'une dérivée d'ordre 2) et ainsi de suite. Nous rencontrerons par ailleurs très fréquemment de telles dérivées en physique (et même en maths pour l'analyse fonctionnelle).
Considérons une dérivée d'ordre 2 telle que:

Si nous regardons le d/dx comme un opérateur différentiel nous pouvons bien évidemment écrire:

Finalement nous avons:

et donc il vient après simplification par f(x):

Les différentielles
Nous avons indiqué précédemment ce qu'était un différentiel d. Mais il existe en fait plusieurs types de sortes de différentielles d'une fonction (remarquez que nous distinguons le genre masculin et féminin du terme):
1. Les différentiels
2. Les différentielles partielles
3. Les différentielles totales exactes
4. Les différentielles totales inexactes
Rappelons que nous appelons "différentiel df" d'une fonction f à une variable la relation donnée par (voir texte précédent):

Cependant, pour exprimer l'effet d'un changement de toutes les variables d'une fonction f de plusieurs variables, nous devons utiliser un autre type de différentiel que nous appelons la "différentielle totale" (dérivée en deux sous-familles: différentielle totale exacte et différentielle totale inexacte).
Soit par exemple, une fonction f(x, y) des deux variables x et y. L'accroissement df de la fonction f, pour un accroissement fini de x à x+dx et de y à y+dy est:

que nous pouvons aussi écrire:

ou :

Pour des accroissements infiniment petits de x et y:

Le premier terme de gauche, nous le voyons, ne donne finalement que la variation en x de la fonction f(x,y) en ayant y constant sur la variation. Nous notons cela dès lors (si la connaissance des variables constantes est triviale, nous ne les indiquons plus):

et de même:

Les deux "différentielles partielles" ou plus simplement "dérivée partielle" sont donc :


Il vient dès lors:

qui est la "différentielle de f". Les thermodynamiciens parlent souvent eux de la "différentielle totale exacte de f" ou plus simplement "différentielle exacte de f".
En fait, la relation précédente est un cas particulier de ce que les mathématiciens appellent en toute généralité une "forme différentielle":

Soit sous forme d'un champ vectoriel :

Remarque: De la même manière, pour une fonction de plus de deux variables, par exemple f(x, y, z), la différentielle totale df est:

Dans l'équation ci-dessus, la différentielle df a été calculée à partir de l'expression de la fonction f. Puisqu'il existe une fonction f qui vérifie l'expression de df, la différentielle df est dite alors aussi "totale exacte".
Notons une indication importante sur l'utilisation des dérivées partielles par les physiciens. Nous avons vu plus haut que si f dépend de deux variables x, y nous avons:

et s'il ne dépend que d'une variable nous avons alors:

et alors:

Il faut donc faire attention de ne pas mélanger les deux notations.
Maintenant, il faut cependant savoir qu'il existe également des différentielles totales exactes qu'aucune fonction ne vérifie. Dans ce cas, nous parlons de "différentielle totale inexacte" et pour déterminer si une différentielle totale est exacte ou inexacte, nous utilisons les propriétés des dérivées partielles (cas très important en thermodynamique)
Reprenons la forme différentielle générale (cela fait appel à de la géométrie différentielle):

où M(x, y) et N(x, y) sont des fonctions des variables x et y. Si dz est une différentielle totale exacte, alors:

On en déduit :


ou encore, en effectuant une seconde dérivation, que:


pour que la forme différentielle, soit une différentielle totale exacte.
Or d'après le "théorème de Schwarz" (mais qui a été démontré à la fin du 17ème siècle par un des frères Bernoulli), soit une fonction f, si:

sont continues alors nous avons un résultat très important dans la pratique:

pour tout (x0,y0) ∈ U où U est le domaine de définition où f est continue (et donc dérivable). Soit, si f s'exprime sous forme différentielle totale exacte alors les différentielles croisées sont égales (la réciproque n'est pas forcément vraie).
Donc pour en revenir à notre problème initial, nous avons :

Ce qui nous donne finalement la "condition de Schwarz":

C'est donc la condition que doit satisfaire une forme différentielle pour être une différentielle totale exacte et la condition qu'elle ne doit pas satisfaire pour être une différentielle totale inexacte. Afin de ne pas confondre les deux types de différentielles, nous utilisons le symbole pour représenter δ une différentielle totale inexacte:

et d pour une différentielle totale exacte:

La distinction est extrêmement importante car seules les différentielles totales exactes qui satisfont donc:

ont une intégrale qui ne dépend que des bornes d'intégration (puisque toutes les variables changent en même temps). Dès lors les différentielles totales inexactes dépendent des bornes d'intégration, ce qui signifie que:

et donc:

Alors que (voir l'autre partie traitant des intégrales curvilignes):

soit :

Autrement dit, la variation d'une fonction dont la différentielle est totale exacte, ne dépend pas du chemin suivi, mais uniquement des états initiaux et finaux car elle s'exprime comme le gradient d'une fonction (par exemple en Électrostatique quand nous vérifions que la différence de potentiel est indépendante du chemin). Nous appelons une telle fonction qui satisfait à une différentielle totale exacte en physique, une "fonction d'état" et en mathématique une "fonction holomorphe" c'est-à-dire une fonction dont la valeur ne dépend que de l'état présent et futur, et non de son histoire.
Par exemple, en thermodynamique, le travail élémentaire d'une force exercée sur un corps en mouvement dans le plan Oxy est donné par :

Fx et Fy ne dérivent pas nécessairement d'un même potentiel U(x, y) tel que:

δW est donc une différentielle totale inexacte.
Dérivées usuelles
Nous allons en démontrer une puis exposer directement le résulat des autres :
Dérivée de x³ :
Soit donc a un réel quelconque fixé, alors:

Le nombre dérivé en a de la fonction cube est donc :

Nous pouvons généraliser ce résultat pour tout entier naturel positif ou négatif n et nous allons voir que la fonction f définie sur ℝ par f(x) = x^n est dérivable et que sa dérivée f' est définie par f'(x) = n x^n-1 :

Ainsi, nous avons (quelques exemples peuvent être utiles pour comprendre la portée de ce résultat):

Nous voyons donc qu'en ayant déterminé la dérivée d'une fonction de la forme x^n, nous avons également déterminé la dérivée de toute fonction qui est mise sous cette forme tel que:


Cependant ces fonctions ne sont pas dérivables en x= 0 puisque la fonction n'y est plus définie (division par zéro). De plus, en ce qui concerne la fonction comportant la racine (puissance non entière), la dérivée n'est pas définie dans ℝ-


2. Calcul intégral
Nous allons aborder ici les principes élémentaires et de base du calcul intégral.
Intégrale définie
L'idée première du concept d'intégral est de calculer l'aire algébrique (surface) entre une courbe et son support:

Une valeur approchée de l'aire sous une courbe peut être obtenue par un découpage en n bandes rectangulaires verticales de même largeur. En particulier on peut réaliser un encadrement de cette aire à l'aide d'une somme majorante AM et d'une somme minorante Am pour un découpage donné :

Supposons que le nombre n de bandes tende vers l'infini. Comme les bandes sont de même largeur, la largeur de chaque bande tend vers 0.
Si les sommes AM et Am et ont toutes deux une limite lorsque, le nombre n de bandes, tend vers l'infini, alors l'aire A sous la courbe est comprise entre ces deux limites. Nous avons:

Si ces deux limites sont égales, leur valeur est celle de l'aire sous la courbe.
D'où une première définition directe de l'intégrale définie ou dite "intégrale de Riemann":
Soit un intervalle [a, b], divisé en n parties égales, soit f une fonction continue sur l'intervalle [a, b], soit Am, la somme algébrique minorante et soit AM, la somme algébrique majorante. Nous appelons "intégrale définie" de f, depuis a jusqu'à b, notée:

Le nombre A tel que:

pourvu que cette limite existe. Si cette limite existe, alors nous disons que f est "intégrable" sur [a, b] et l'intégrale définie existe.
Les nombres a et b de l'intégrale sont appelés les "bornes d'intégration": a est la "borne inférieure", b est la "borne supérieure".
Intuitivement, il est évident que lorsque b=a, nous étendons la définition ainsi:

Il existe une deuxième approche de définition de l'intégrale où nous utiliserons cette fois-ci, le S de la surface au lieu du A de l'aire.
Nous pouvons calculer l'intégrale de Riemann avec la méthode des rectanges à gauche par cumul de la surface des "rectangles à gauche" de largeur ∆xᵢ = xᵢ - xᵢ-1 de plus en plus petite :


Nous obtenons ainsi la surface totale de la courbe voulue :

Le fait de chercher cette limite s'appelle "calculer l'intégrale", et plus spécifiquement de la méthode choisie: "intégrale de Riemann".
Intégrale indéfinie
Nous avons vu précédemment lors de notre étude des dérivées, le problème suivant: étant donnée une fonction F(x), trouver sa dérivée, c'est-à-dire la fonction:

Définition: Nous disons que la fonction F(x) est une "primitive" ou "intégrale indéfinie" de la fonction f (x) sur le segment [a, b], si en tout point de ce segment nous avons l'égalité F'(x) = f(x)
Une autre manière de voir le concept d'intégrale indéfinie est de passer par le "théorème fondamental du calcul intégral (et différentiel)" appelé aussi parfois "théorème fondamental de l'analyse" dont les 2 propriétés s'énoncent ainsi:
Soit f une fonction continue sur un intervalle fermé [a, b].
Si A est la fonction définie par
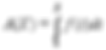
pour tout X dans [a, b], alors A est la primitive de f sur [a, b] qui s'annule en a (ou en d'autres termes: f(t) est la dérivée de A)
Si F est une primitive de f sur [a, b], alors :

Il résulte de ces propriétés que si nous connaissons une primitive quelconque F(x) de la fonction f(x), toute autre primitive de cette fonction sera de la forme:

Donc finalement, nous appelons "intégrale indéfinie" de la fonction f(x) et nous notons:

Donc si et seulement si F'(x) = f(x) nous avons :

Géométriquement, nous pouvons considérer l'intégrale indéfinie comme un ensemble (famille) de courbes telles que nous passons de l'une à l'autre en effectuant une translation dans le sens positif ou négatif de l'axe des ordonnées.
Voici quelques propriétés utiles de l'intégration :
La dérivée d'une intégrale indéfinie est égale à la fonction à intégrer:

La différentielle d'une intégrale indéfinie est égale à l'expression sous le signe somme:

L'intégrale indéfinie de la différentielle d'une certaine fonction est égale à la somme de cette fonction et d'une constante arbitraire:

L'intégrale indéfinie de la somme (ou soustraction) algébrique de deux ou plusieurs fonctions est égale à la somme algébrique de leurs intégrales:

Nous pouvons sortir un facteur constant de sous le signe somme, c'est-à-dire:

Nous pouvons sortir un facteur constant de l'argument de la fonction intégrée (plutôt rarement utilisée):

L'intégration d'une fonction dont l'argument est sommé (ou soustrait) algébriquement est la primitive de l'argument sommé (respectivement soustrait):

La combinaison des 2 précédentes propriétés nous permet d'écrire:

Soit f une fonction continue sur [a,b], nous avons pour tout c appartenant à cet intervalle:

Intégrale double
L'idée des intégrales doubles est de mesurer le volume de la zone délimitée par le graphe d'une fonction de deux variables, au-dessus d'un domaine D du plan (ci-dessous D est rectangulaire).

Là encore, l'idée est la même que l'intégrale définie. Si nous adaptons une approche simpliste, nous décomposons la fonction continue en un escalier et le volume à calculer se réduit alors à faire la somme des volumes de parallélépipèdes:


Pour une fonction continue, nous procèdons par approximations successives: nous calculons des sommes de Riemann pour des subdivisions de plus en plus fines du domaine D:


Par contre, quand on veut intégrer sur un domaine qui n'est pas rectangulaire, les choses se compliquent. Voyons comment contourner le problème :
Pour cela, nous allons construire le domaine D fermé borné de la façon suivante :

où le lecteur aura remarque que le support de y est la variable x par l'intermédiaire de deux fonctions u et v. C'est ce que nous appelons alors un "domaine du type I" (et donc si c'est y qui paramétrise x alors il s'agit domaine de type II).
Ce qui peut s'illustrer par la figure ci-dessous:


Donc nous transformons l'intégrale double en deux intégrales simples emboîtées.
Intégration par changement de variables
Lorsque nous ne pouvons facilement déterminer la primitive d'une fonction donnée, nous pouvons nous arranger par un changement de variable astucieux (parfois même très subtil) pour contourner la difficulté.
Soit à calculer l'intégrale (non bornée pour l'instant):

bien que nous ne sachions pas calculer directement la primitive de cette fonction f(x) (en tout cas nous imaginons être dans une telle situation) nous savons (d'une manière ou d'une autre) qu'elle existe (nous ne traitons pas encore des intégrales impropres à ce niveau).
La technique consiste alors dans cette intégrale à effectuer le changement de variable:

où φ(t) est une fonction continue ainsi que sa dérivée, et admettant une fonction inverse. Alors dx = φ'(t) dt, démontrons que dans ce cas l'égalité:

est satisfaite.
Nous sous-entendons ici que la variable t sera remplacée après intégration du membre droit par son expression en fonction de x. Pour justifier l'égalité en ce sens, il suffit de montrer que les deux quantités considérées dont chacune n'est définie qu'à une constante arbitraire près ont la même dérivée par rapport à x. La dérivée du membre gauche est:

Nous dérivons le membre droit par rapport à x en tenant compte que t est une fonction de x. Nous savons que:

Nous avons par conséquent:

Les dérivées par rapport à x des deux membres de l'égalité de départ sont donc égales.
Bien évidemment, la fonction x = φ(t) doit être choisie de manière à ce que nous sachions calculer l'intégrale indéfinie figurant à droite de l'égalité.
Intégration par parties
Lorsque nous cherchons à effectuer des intégrations, il est très fréquent que nous ayons à utiliser un outil (ou méthode de calcul) appelé "intégration par parties". Il existe différents degrés d'utilisation de cet outil et nous allons commencer par le plus simple et qui est le plus utilisé dans tous les chapitres traitant de physique sur le présent site.
Nous partons d'abord de la dérivée du produit de deux fonctions démontrée plus haut:

nous avons donc:

et il vient:

après une dernière simplification nous avons enfin la fameuse relation très importante utilisée par exemple dans la section dédiée à la relativité restreinte :

Primitives usuelles

Intégrales curvilignes
Ces intégrales sont très importantes en Physique, en particulier dans le chapitre des Calculs Vectoriels qui sera traité plus tard.
Intégrale curviligne d'un champ scalaire
Considérons une courbe C paramétrée par une fonction vectorielle r(t) avec t ∈ [a,b] de classe C1 (cette condition est nécessaire pour que l’on puisse intégrer sur la courbe sans problèmes) :
La courbe est dite "courbe fermée" si

La courbe est dite "courbe régulière" si

Une courbe paramétrée peut être écrite sous la forme suivante (toute fonction vectorielle peut être écrite sous cette forme):

Considérons une fonction ou un "champ scalaire" f(x,y) définie dans un voisinage de C. Subdivisons [a,b] en n sous-intervalles ∆t de même longueur tel que:

Nous choisissons sur chaque sous-intervalle un point :

Soit ∆Si la longueur de l'arc de C reliant les points (x(ti),y(ti)) et (x(ti+1),y(ti+1)), l'intégrale de f le long de C est définie comme étant "l'intégrale curviligne" ou "intégrale de chemin":

Ce qui peut s'écrire :

En sachant que l'abscisse curviligne différentielle d'une courbe plane (plan dans un espace euclidien dans ℝ²) est donnée par (que nous verrons plus en géométrie différentielle) :

Et qui peut évidemment être étendu au cas à 3 variables et plus la sous forme vectorielle:

L'intégrale curviligne est linéaire, c'est-à-dire que si C = C1 U C2 et C1 ∩ C2 est un point:

Intégrale curviligne d'un champ vectoriel
Considérons un champ de vecteur (par exemple un champ de force) tel que:

et une élément infinitésimal d'une courbe C1 en 2D tel que :

L'idée est alors de considérer que le produit scalaire (projection de champ vectoriel sur l'élément de chemin) représente le travail le long de l'élément différentiel:

Par conséquent le travail sur tout le chemin sera donné par (en utilisant au passage la propriété de linéarité de l'intégrale):

Ce qui peut se généraliser à n dimensions. Notons que lorsque l'intégrale curviligne (de chemin) d'un champ vectoriel est étendue à une courbe fermée, nous parlons alors de "circulation du champ vectoriel".
Etant donné que :

NOus pouvons en déduire que :

Il faut savoir qu'en physique, on opère souvent en coordonnées polaires plutôt qu'en cartésienne afin de faciliter les calculs.
Exemple :
Calculons le travail de la force de pesanteur déplaçant une masse M du point M1(a1,b1,c1) au point M2(a2,b2,c2) le long d'un chemin arbitraire C. Les projections de la force de pesanteur sur les axes de coordonnées sont:

Le travail accompli est alors:

Or Une intégrale curviligne d'un champ vectoriel F le long d'une courbe C1 est indépendante du chemin d'intégration si:
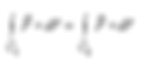
pour toute courbe C2 ayant les mêmes points de départ et d'arrivée. De plus, si le champ de vecteurs satisfait (où G est un potentiel gravitationnel dont on estime le gradiant):

Dont la forme différentielle totale exacte est, rappelons le :

Donc rappelons le, l'intégrale de chemin sur une courbe dépend uniquement de la différence des valeurs de la fonction G aux deux extrémités.
En effet, si la forme différentielle du champ de vecteur satisfait bien une différentielle totale exacte, nous avons:

Donc l'intégrale curviligne d'une différentielle totale exacte ne dépend pas du chemin d'intégration mais seulement des extrémités. Nous en déduisons également que si F dérive donc d'un potentiel scalaire et que A = B, l'intégrale curviligne est alors nulle.
En physique ce résultat s’interprète en disant que le travail fourni par une force F dérivant d'un potentiel scalaire s'exerçant sur une particule élémentaire lors d'un déplacement fini ne dépend pas du chemin suivi.
Définitions :

Lorsque la courbe C est fermée et que l'intégrale de chemin a un résultat indépendant du sens dans lequel ce chemin est parcourue, nous utilisons la notation (la lettre sous l'intégrale pouvant varier). Si cette intégrale fermée est toujours nulle, nous disons que le champ vectoriel intégré est un "champ conservatif" et "dérive d'un potentiel scalaire" (et donc satisfait le théorème de Schwarz pour pouvoir être écrit sous forme de différentielle totale exacte) puisque ceci découle de la démonstration donnée déjà juste plus haut.

Lorsque la valeur de l'intégrale de chemin fermée dépend du sens de parcours, nous utilisons la notation suivante (la lettre sous l'intégrale pouvant varier).
Ainsi, pour résumer, une intégrale curviligne (de chemin) est entièrement définie par l'expression sous le signe de l'intégrale, la forme de la courbe d'intégration et le sens d'intégration.


