Théorie des systèmes dynamiques
- Tutux
- 16 févr. 2023
- 6 min de lecture
Dernière mise à jour : 23 déc. 2023
La théorie des systèmes dynamiques est une branche des mathématiques qui étudie les phénomènes de mouvement et de changement dans le temps. Elle cherche à comprendre comment les systèmes évoluent en fonction de leurs conditions initiales et des forces qui s'exercent sur eux.
La géométrie symplectique est une combinaison de cette théorie est de la géométrie différentielle (qui étudie les formes et les propriétés des espaces courbes. Elle s'intéresse en particulier à la manière dont ces espaces se déforment et se plient sous l'influence de forces extérieures), basée sur la formulation hamiltonienne de la mécanique classique. Elle étudie des objets mathématiques appelés "variétés symplectiques" qui ont une structure particulière permettant de mesurer des tailles. Contrairement à la géométrie riemannienne qui utilise un outil appelé tenseur métrique pour mesurer des longueurs et des angles, la géométrie symplectique utilise une forme mathématique appelée "forme symplectique" pour mesurer des aires.
Jean-Marc Souriau était un des grands pionnier de cette géométrie topologique symplectique en développant la notion de quantification géométrique, qui permet de faire émerger des quantités fondamentales de la physique (comme l'énergie et le moment) en tant qu'objets purement géométriques. Il a su donner la véritable signification physique de l'inversion de la flèche du temps reprise dans notre modèle cosmologique (Voir section T-symétrie).
Qu'est-ce qu'un groupe ?
Mathématiquement, il s'agit simplement de certaines matrices agissant sur d'autres matrices. Mais physiquement, qu'est-ce que celà représente ?
Selon J-M Souriau, un groupe est créé pour transporter et la façon de transporter est plus importante que ce qui est transporté : "Dis-moi comment tu bouges, je te dirai qui tu es"
Nous allons nous intéresser principalement aux groupes de Lie qui sont à la fois des groupes et des variétés différentielles (variétés "espaces courbes" localement projetés sur un espace euclidien de dimension n). Ils sont utilisés pour décrire les mouvements et les transformations dans l'espace. Les deux groupes mentionnés sont le groupe orthogonal O(3) et le groupe euclidien E(3).
Le groupe orthogonal O(3) est utilisé pour décrire les rotations et les symétries en trois dimensions, et il préserve les distances dans l'espace. Il contient un sous-groupe important appelé SO(3), qui est également connu sous le nom de groupe de rotation, car il gère les rotations autour d'un axe.
Le groupe euclidien E(3) est un groupe qui décrit les mouvements en trois dimensions, tels que les rotations, les symétries et les translations. Il est construit sur le groupe orthogonal O(3), et peut être décomposé en une force et un couple appliqué sur un objet en mécanique des solides. Il s'agit d'un groupe à l’intérieur duquel, on peut calculer une longueur entre 2 points grâce au théorème de Pythagore. Ce groupe va permettre de transformer un point de coordonnées x y z en un point de coordonnées x’ y’ z’. La particularité de ce groupe dynamique c’est qu’il va nous permettre de générer toute une famille d’objets géométriques qui sont invariants dans ce groupe. Par exemple, si on imprime une translation à une droite, elle restera une droite donc la droite est un objet géométrique à 1 dimension invariant. La sphère est également un objet géométrique 3D qui reste invariant car lorsqu'on lui imprime une rotation autour de son centre elle reste « elle même », on dit qu’elle se parcourt elle même, sa métrique en tout point de celle ci est symétrique ce qui veut dire que la grandeur conservée sur celle ci est le mouvement donc sa dérivée ou la vitesse est une grandeur conservée au cours du temps tout autour de celle ci. Autre exemple, l’hypersurface 3D intérieure de Schwartzschild est une sphère qu'on peut considérer comme invariante mais dans un autre groupe dynamique qui est celui de minkowski ou de poincare (équivalent du groupe euclidien mais dans l’espace relativiste). Par conséquent, toute géodésique la parcourant aura une métrique dont la dérivée par rapport au temps sera conservée dessus.
Les groupes de Lie permettent donc de décrire les mouvements dans l'espace tout en préservant les distances et les longueurs. Ils sont des groupes d'isométrie lorsque les propriétés géométriques des objets en mouvement restent inchangées (distances et angles) dans l'espace lorsqu'on leur applique une transformation. Les rotations sont donc des exemples de symétries de l'espace tridimensionnel, car elles ne changent pas les propriétés géométriques de celui-ci. Par exemple, si vous prenez un cube et que vous le faites tourner, les distances entre les sommets du cube restent les mêmes. En d'autres termes, les propriétés géométriques de l'objet restent inchangées, bien que sa position ait été modifiée.
Selon la théorie de la relativité restreinte, au lieu de vivre dans un espace euclidien à 3 dimensions [x, y, z] de signature (+ + +) où le temps est une entité séparée, nous vivons en réalité dans un espace à 4 dimensions où les trois dimensions de l'espace sont perpendiculaires à une dimension du temps, dans un espace-temps unique [t, x, y, z] appelé espace de Minkowski, de signature (- + + +).
Le groupe dynamique associé à cet espace est celui de Poincaré. Il va nous permettre d'engendrer des mouvements particuliers comme par exemple des mouvements de particules à masses nulles que sont les photons (car ils ne sont jamais au repos mais toujours à la même vitesse qui est celle de la lumière, ils ne peuvent être freinés ou ralentis par la gravité, il n’y a donc que son énergie qui peut être modulée) et la famille des particules à masses non nulles :



Le groupe dynamique de Poincaré est le groupe appliqué à la relativité restreinte qui inclut le mouvement des masses ou photons avec une flèche du temps en opposition possible c’est-à-dire du passé vers futur et inversement. En effet, la moitié des éléments du groupe dynamique inverse le temps, ce qui veut dire que si l'on considère un élément de l’espace-temps comme une masse ou un photon et qu’on lui imprime un mouvement temporel du passé vers le futur, on peut obtenir le même mouvement dans l’autre sens en lui appliquant le groupe de Poincaré. Par conséquent, selon la théorie de Souriau tiré de son ouvrage Structure des systèmes dynamiques, si le groupe dynamique peut faire circuler des photons ou des masses avec une flèche du temps en opposition alors leur énergie, et donc leur masse peuvent également s’inverser :


On peut représenter ce groupe dynamique sous forme de matrices :

Désormais, peut-on maintenant considérer ces mouvements à énergie et masse négatives avec une flèche du temps en opposition comme faisant partis de la Physique ? Peut on les mesurer ou les observer ?
Ces particules d’énergie négative émettent des photons d’énergie négative donc on ne peut pas les observer ni les mesurer optiquement.
Or on a constaté et mesuré que l’expansion de l’univers s’accélérait sous l’effet d’une pression négative liée à une énergie noire (Perlmutter - Prix Nobel 2011). La pression étant une densité d’énergie par unité de volume :

L’expansion de l’univers est donc directement liée à une énergie négative.
Cela signifie qu’une énorme partie de l’univers actuellement définie comme étant la matière sombre à énergie noire agit sur cette expansion par effet gravitationnelle. Ce groupe dynamique et cette approche géométrique permet donc d’apporter une réponse sur son origine et sa nature. Il peut donc s’agir d’un contenu à masses ou photons chargés avec une énergie négative.
Pour gérer les mouvements de particules chargées dans ce groupe dynamique, il faut ajouter une dimension supplémentaire pour aboutir à ce qu’on appelle un groupe de Kaluza composé de matrices ayant la forme suivante :
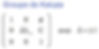
Pour gérer cette CPT-symétrie, nous proposons un nouveau groupe qu’on appelle le groupe Janus :

Ce nouveau groupe montre qu’il y a 2 antimatières au lieu d’une :
C-symétrie : Antimatière à masse positive au sens de Dirac bien connue qu’on est capable de reproduire (C : charge qui s’inverse)
PT-symétrie : Antimatière de masse négative au sens de Feynman à cause de la T-symétrie qui échappe à l’observation et ne révélant sa présence que par effet gravitationnel (P : parité à savoir que les entités physiques sont énantiomorphes et T : le temps qui s’inverse)
Un peu de géométrie appliquée au modèle...
Lorsqu'on considère un tore auquel on retire une portion d'angle θ puis que l’on raccorde ensuite, on forme un Posicône. Si l'on souhaite le joindre à une calotte sphérique de sorte que les plans tangents soient confondus, il faut que le posicône soit réalisé avec un angle de courbure θ égale à celui de la calotte sphérique. Or, si on considère une calotte sphérique de surface "s" prise dans une sphère de surface "S" et de courbure 4 π, elle aura un angle de courbure égal à 4 π s / S, donc l'angle de courbure du posicône doit être égal à la même valeur pour les raccorder :

Le Negacône est l’inverse à savoir un tore auquel on rajoute la même portion de rayon de courbure θ et que l’on replie pour former une selle de cheval de rayon de courbure négatif.
Pour mesurer la quantité de courbure d'une surface, il faut utiliser un curvimètre de Riemann qui est en fait un tore dont on gradue une portion d'angle de courbure que l'on retire ou que l'on ajoute en fonction de la surface courbée dont on souhaite mesurer la quantité de courbure. Par exemple, pour le negacône, on va graduer cette portion d'angle de courbure que l'on retire au tore dans le sens inverse des aiguilles d'une montre. Pour le posicône, la graduation se fera dans le sens des aiguilles d'une montre. Ensuite on applique ce curvimètre sur la surface courbée dont on souhaite connaître l'angle de courbure θ.
Les 2 géométries conjuguées forment des densités de courbures opposées :

Un photon parcourant un posicône verrait sa géodésique courbée positivement tandis qu’elle sera courbée négativement le long du negacône conjugué :



